Knowing About the World via GIS

Geography is the study of the earth and its’ features, inhabitants, and phenomena, which is a discipline system studying the interaction, changes and spatial difference in all spheres of earth surface system. So, about 80% of everyday information is strongly related to the geographic position, and can all be called Geographic information.

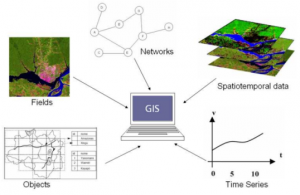
GIS is a comprehensive technology system used for collecting, processing, management, analysis, expression and transmission of geographic information. The strong capabilities of data analysis and processing make GIS like the brain of Geography. Therefore, GIS can be a key platform not only for Geography research but also for social services. Until now, GIS is applied to various areas like resource investigation, environmental assessment, disaster prediction, land management, transportation, military police, water conservancy and so on.

To a country, GIS is closely linked to national development and security. For example, when first Gulf War broke out, the US military had won a decisive victory at a modest price, hitting the Iraqi army with a precise strike. The City GIS system of Iraqi, which is built with the help of U.S., provides critical battlefield geographic information to the U.S., largely determining the outcome of the war.

To industry applications, GIS undoubtedly enhances the production efficiency. Let’s take China’s logistics industry as an example. GIS established a perfect management system for it, which includes supply management, personnel management, path planning and so on. So, everyone can sit at home to buy all the things from Internet and then get your commodities after one or two days. To everyone’s daily life, “Uber Taxi” may be one of the best examples of GIS applications. People can search the taxi at service nearby, plan the route to your own destination with real-time calculated prices and query for interest points around all by smartphones, which profoundly changes the way travel.

GIS is an interdisciplinary science and makes use of many advanced achievements of Engineering and Computer Science. The major branches directly related to GIS applications I think are Topography, Graphics, Data Science and High-performance heterogeneous computing. Topography provides the data source and measurement calculation methods to GIS, and Data Science instructs the data storage, management, and analysis process of GIS data models. Graphics provides strong tools for GIS visualization. At last, High-performance heterogeneous computing gives GIS an efficient method for calculating, which is the energy of GIS applications.

According to the characteristics of GIS mentioned above, geographical objects expression and computation based on Euclidean geometry are highly dependent on object coordinates and coordinate systems and the expression and analysis of different dimensional geographical objects are at disunity. So, we need to find out a corresponding unified coordinate system to represent the geographical objects of a different scale from global to local. In GIS, we are not only studying the geographical objects but also the geographical phenomena and geographical process. Geographical phenomena and process are usually characterized as multidimensional features and span many different spatio-temporal scales. Moreover, as the fusion analysis of geometric objects with different dimensions, it is rather difficult to be linked and integrated effectively with geographical models. All in all, in GIS, we have got a lot of multi-source heterogeneous data which is referenced as geometry and developed much more analysis models which are referenced as algebra, but they cannot be integrated appropriately.

Based on philosophical and physical considerations, it seems that only Geometry Algebra can solve these problems effectively. As a unified descriptive language, GA can connect algebra and geometry, mathematics and physics, abstract space-time and entity space-time. So, introducing GA to GIS has a prospective to improve the multidimensional expression and analysis ability of GIS.

Products in GA define spatial operation sets as geometries, measurements, topologies and directions, and have the ability to achieve expression and mutual transformation among various kinds of space, and thus support unification and expression of various algebra and geometric system. Under the GA framework, operation rules and operators are designed to support the complex geometric calculation, in order to construct GIS computing engine based on GA.

The ability of geometric computation and expression in GA makes time an equivalent dimension to space in computational space construction, thus the expression and computation of unified time and space are achieved. For example, if we want to track a ship moving in the ocean together with cameras (optical remote sensing), sonar (acoustic remote sensing) and radar (electromagnetic remote sensing), we have to deal with images, waves, and fields with different speeds through very large scales, we need to integrate different spatio-temporal references. And classical Euclidean geometry will be invalid for this situation due to numerical computational precision. However, with GA, we can easily deal with this situation using frame-based representations and versors like what we have already done in spacetime algebra.

GA intrinsically mixes the dimensional computation of definite geometric meaning, achieves integrative expression and storage of objects of different dimensions in mathematical structures, and supports expression, modeling, and analysis of complex geographical phenomena and geographical process.

GIS data models and analysis models can also be extended in GA framework, which will help to build a unified descriptive framework of multidimensional geographical time and space. Besides, present analysis models and algorithms such as statistical model, dynamic model, and differential equation model can be inherited and unified to support geographical models and compact integration of GIS analysis and geographical analysis.

The real world is complex, so does the geographic information obtained from the world. GIS is considered as a common platform, which needs a spatio-temporal coordinate system, static or dynamic state, and geographical phenomena or process. This condition leads to the huge amount of heterogeneous data, geometric or algebraic expressions, and analysis models. So, the difficulties of creating good GIS simulators I think maybe in four aspects:

(1) How to develop a unified spatio-temporal framework that can integrate geographical objects, phenomenon and geoscience data at different scales with different characteristics? How to make the translation and coupling of the global spatio-temporal framework/reference with a local or several local frameworks/references seamlessly.

(2) How to develop an efficient scene-based data model that can not only have enough power to represent real geographic objects/phenomenon in a parametric way but also can support efficient organization, storage, computation and visualization in current computer framework.

(3) How to integrate users with different requirements (e.g. geographer, common publics, policy makers, developers and computer scientists) with a common, flexible but powerful expression and computation language, which can both easy use but also efficient for dynamical computing.

(4) How to deal with dynamical simulation and continues data updating and visualization by coupling various different geographical models. How can we combine them in an integrating framework and make them work together.

The above three conflicts all points to one thing: that a transmission tool is an urgent need. So, Geometric Algebra is found from the areas of mathematics and physics to act as a convergence tool. The unity of geometry and algebra, time and space, different dimensions, expression and computation of GA is just as the effective way to solve the existing problem.

In our past work, we have done the Multi-dimensional complex object expression based on Blade, the Multi-dimensional complex scenes expression based on Multivector, and the Multi-dimensional unified computation based on geometric algebra, which laid the foundation for the new GIS simulator through the data structure, expression, and calculation.

GA can effectively represent the relationship and measurement of different shapes, and Multivectors can realize the integration and unification of different dimensions and types of geometric objects. Then in the computation part, GA calculation is almost based on operators, which have good compatibility with various analysis models, such as dynamic model or differential equation model. A famous example is the expression of Maxwell’s equation, which can be transformed into a single equation by GA. So, to geographic computation, it’s of great significance to integrating and optimizing the existing models.

In the GA simulation, a series of compilers can be created to translate all these models into GA expressions, and then into the C++ codes, which improves the efficiency and reduces the computational complexity. On the basis of those compilers, high-performance heterogeneous parallel computing can also be easily realized. Above all, GA does the overall rebuild to the old simulators and makes GIS simulators more efficient, concise and smart.

In GAGIS, the most impressive thing for me is that all of the researchers had done excellent works in their research area. Because of the characteristics of GIS, It attracts people in many directions and fields. During the meeting, each researcher made a wonderful report and after the report, the participants put out a lot of questions and I also learned much about it from their response. On the last day of the meeting, we also visited the laboratory and learn about the wonderful work that they had done.

As a common platform, GIS has the potential to support the development and application of geometric algebra and its related fields as a representative work. For example, image processing can rely on the GIS platform to design the corresponding image processing algorithms and validate it directly with GIS data. However, until now, all we have done is primary, and we need to collaborate with the international GA and GIS related researchers. We also want to show our work to the international society and attract more researcher to join us, letting them collaborate with us under this framework.

Before the conference, I expected to learn more about geometric algebra in various fields of research and introduce our achievement to everyone in order to attract more intelligent people to join us. And now, it works. From the perspective of geography at home and abroad, GA is high-profile in GIS because of the characteristics of GIS itself. There are a series of teams doing the research about it and there are some projects supporting it. Unfortunately, international geometric algebra teams are relatively dispersed. How to unite this group of people to form a complete organization is the key point to promote the development and influence of GA. The most important thing that I want to say is that international conference is important to publicize what we do and strengthen communication, publicity, and cooperation. That is what we have never done before.