Edifying The Young

I have taught and published in several different areas of mathematics and physics. I faced no serious obstacles in pursuing my varied interests (except to find more than 24 hours in a day). Lucky!

I read strong claims about geometric algebra and decided to look for myself. I was smitten. I found that geometric algebra and its extension to geometric calculus unify, simplify, and generalize vast areas of mathematics involving geometric ideas, including linear algebra, vector calculus, complex analysis, exterior algebra and calculus, tensor algebra and calculus, quaternions (3D spinors), and euclidean, non-euclidean, and projective geometries. I also found that GA provides a common mathematical language for many areas of physics (classical and quantum mechanics, electrodynamics, special and general relativity), computer science (graphics, robotics, computer vision), engineering, and other fields. People in disparate fields can now talk to each other!

My response: Geometric algebra unifies many of your mathematical tools and works better than any of them. Unfortunately, this has not been sufficient to induce many to switch. GA takes time to learn. And once learned, there is the problem of communicating with others who haven’t learned. Nevertheless, geometric algebra is gaining adherents, slowly but surely.

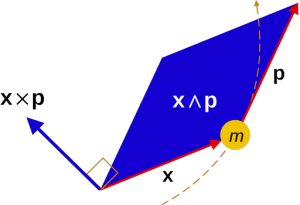
Geometric algebra is a superset of linear algebra, with more objects, multivectors, and more operations; for example, the geometric product. So anything that linear algebra can do geometric algebra can do. Even within linear algebra, geometric algebra brings advantages. Here is a simple example. Consider the orthogonal complement of a subspace: the set of vectors orthogonal to all vectors in the subspace. For both linear and geometric algebra this geometric definition tells us what the orthogonal complement is. Geometric algebra adds algebra, providing a very simple way to compute the complement (as a dual), something linear algebra can’t do. This illustrates the name Geometric Algebra: it does geometry algebraically.

I share David Hestenes’ vision of wide acceptance of GA and the advantages this will bring.

A vital aspect of making this happen is encouraging and enabling GA’s inclusion in the undergraduate mathematics curriculum. The only way that mathematics faculties will consider this is to have available GA texts written in traditional mathematics textbook style. This is my small contribution to Hestenes’ vision.

Mathematicians have been infuriatingly slow in becoming interested in geometric algebra. We are repeating the short-sightedness of 120 years ago when Engineers welcomed Gibbs’s and Heaviside’s vector analysis, though the mathematicians did not ¹.

I chose Alan Bromborsky’s GAlgebra for my texts because it is free, it is multiplatform, it does symbolic calculations, and it is well designed. But it is far from everything I could ask for: its syntax for expressions is sometimes awkward; it requires several other programs, e.g., Python, making installation difficult for some; and it has no graphics capability.

I would like to see a program with GAlgebra’s strengths but not its shortcomings.

My experience is in teaching undergraduate mathematics in the United States, so I will speak to that. Students typically take a year of scalar calculus in their first year of college, then courses in linear algebra and vector calculus in their second year.

The most natural place to introduce GA & GC is right after scalar calculus. I believe that the current second-year linear algebra and vector calculus courses should be renamed Geometric Algebra and Geometric Calculus, their purpose being to provide the basic vocabulary of mathematics in dimensions greater than one. By judiciously trimming the current courses and taking advantage of the simplifications of GA & GC, a lot of GA & GC can be covered. My two textbooks Linear and Geometric Algebra and Vector and Geometric Calculus are attempts at this.

GA & GC are well developed at the elementary level, ready for use. But there are problems to be solved before they can take their rightful place.

We face a chicken and egg problem: students must learn GA & GC to apply them, and those applying vector methods, but not brought up on GA & GC, must push for their inclusion in the curriculum. And if students learn GA & GC in their second year, this cannot be a dead end: instructors in later courses must use them in their courses. Another problem: people are reluctant to publish using a mathematical formalism unknown to most. We can only do our best, making incremental progress until a critical mass is achieved.