2018
“An Extended Implementation Framework for Geometric Algebra Operations on Systems of Coordinate Frames of Arbitrary Signature”
Advances in Applied Clifford Algebras, March 2018 (online)
There is a steadily increasing interest in applying Geometric Algebra (GA) in diverse fields of science and engineering. Consequently, we need better software implementations to accommodate such increasing demands that widely vary in their possible uses and goals. For large-scale complex applications having many integrating parts, such as Big Data and Geographical Information Systems, we should expect the need for integrating several GAs to solve a given problem. Even within the context of a single GA space, we often need several interdependent systems of coordinates to efficiently model and solve the problem at hand. Future GA software implementations must take such important issues into account in order to scale, extend, and integrate with existing software systems, in addition to developing new ones, based on the powerful language of GA. This work attempts to provide GA software developers with a self-contained description of an extended framework for performing linear operations on GA multivectors within systems of interdependent coordinate frames of arbitrary metric. The work explains the mathematics and algorithms behind this extended framework and discusses some of its implementation schemes and use cases. If properly implemented, the extended framework can significantly reduce the memory requirements for implementing Geometric Algebras with larger dimensions, especially for systems based on the symbolic processing of multivector scalar coefficients.
2017
“Introducing Geometric Algebra to Geometric Computing Software Developers: A Computational Thinking Approach” (online)
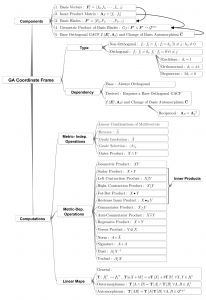Designing software systems for Geometric Computing applications can be a challenging task. Software engineers typically use software abstractions to hide and manage the high complexity of such systems. Without the presence of a unifying algebraic system to describe geometric models, the use of software abstractions alone can result in many design and maintenance problems. Geometric Algebra (GA) can be a universal abstract algebraic language for software engineering geometric computing applications. Few sources, however, provide enough information about GA-based software implementations targeting the software engineering community. In particular, successfully introducing GA to software engineers requires quite different approaches from introducing GA to mathematicians or physicists. This article provides a high-level introduction to the abstract concepts and algebraic representations behind the elegant GA mathematical structure. The article focuses on the conceptual and representational abstraction levels behind GA mathematics with sufficient references for more details. In addition, the article strongly recommends applying the methods of Computational Thinking in both introducing GA to software engineers, and in using GA as a mathematical language for developing Geometric Computing software systems.
2016
Ph.D. Dissertation Book: “Code Generation for Geometric Algebra: Combining Geometric, Algebraic, and Software Abstractions for Scientific Computations” (online)
Geometry is an essential part of almost every solution to problems in computer science and engineering. The process of manually creating geometry-enabled software for representing and processing geometric data is tedious and error-prone. The use of automatic code generators for such process is more suitable, especially for low-dimensional geometric problems. Such problems can be commonly found in computer graphics, computer vision, robotics, and many other fields of application. A mathematical algebraic system with special characteristics must be used as the base of the code transformations required for final code generation. Geometric Algebra (GA) is one of the most suitable algebraic systems for such task. This work describes the design and use of one such GA-based prototype code generation system: GMac. The main function of GMac is to transform a high-level GA-based description of the geometric algorithm into an efficient low-level software code capable of processing the relevant geometric information. The illustrated reduction of design and maintenance efforts provided by GMac is one key to reducing costs of software development for geometry-aware software systems.
2010
Ph.D. Dissertation: “Optimized Automatic Code Generation for Geometric Algebra Based Algorithms with Ray Tracing Application” (online)
Geometry is an essential part of almost every solution to problems in computer science and engineering. The process of manually creating geometry-enabled software for representing and processing geometric data is tedious and error-prone. The use of automatic code generators for such process is more suitable, especially for low-dimensional geometric problems. Such problems can be commonly found in computer graphics, computer vision, robotics, and many other fields of application. The main function of a geometric code generator is to transform a high-level description of the geometric algorithm into an efficient low-level software code capable of processing the relevant geometric information. A high-level geometric Domain Specific Language (DSL) is used for coding the input to the code generator. A mathematical algebraic system with special characteristics must be used as the base of the DSL and the transformations required for final code generation. Geometric Algebra (GA) is one of the most suitable algebraic systems for such task.
This work illustrates the use of GA as the base for creating a geometric software code generator for low-dimensional geometric problems. The proposed code generator, called GMac, is compared to other similar GA-based code generators. The comparisons are made between the code generators architectures, in addition to the performance of generated code. The proposed code generator is applied in a ray tracing application to enhance its features and performance. The results compare well with traditional approaches based on vector and matrix algebras. The net result is the ability to easily create efficient implementations for GA-based algorithms for solving low-dimensional geometric problems. Such GA-based algorithms require less memory, less processing power, less design effort, and less debugging and maintenance. The reduction of design and maintenance efforts is the key to reducing the cost of software development for geometry-aware software systems.
2004
M.Sc. Thesis: “Combined Classifiers for Invariant Face Recognition” (online)
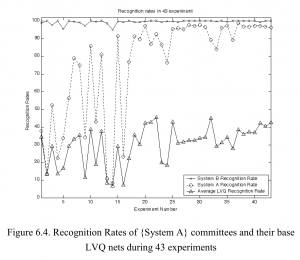Among all the problems of pattern recognition, face recognition is one of the most difficult ones. The special nature of this problem required the researchers to investigate many classification approaches to solve this problem. No single classifier is able to perform equally well under all the various forms of face recognition applications. The only proof of the existence of such a classifier is the human brain with its enormous recognition capabilities. Since the idea of combining multiple classifiers appeared, it triggered a huge number of attempts to apply it to many pattern recognition problems. In this technique, a number of base classifiers are separately trained on the problem and their decisions are then combined using some combination strategy. Although there is no combined system able to remove all the difficulties of the face recognition problem, the combined classifiers techniques proved to possess very interesting attributes that can eventually remove many obstacles in the way of obtaining a good solution for such a complex problem. Nevertheless, the weaknesses of the base classifiers are reflected on the final combined systems. Base classifiers that are complex to design, possess low recognition rate, or have low stability can greatly affect the complexity, performance, and stability of the resulting combined system. In this work, a system for combining unstable, low-performance classifiers is proposed. The system is applied to classify face images from a face database containing 392 persons. The proposed system shows remarkable stability and a high recognition rate using a reduced number of design parameters. The system is better than many of the combined classifiers systems reported in the literature in its simplicity, stability, recognition rate, and scaling with increased input size. The proposed system can be implemented on an ordinary PC and is suitable for multimedia human-computer interaction applications. The proposed system can also be implemented using parallel processing techniques to handle a large number of persons. This work illustrates the possibility of designing a combined system that benefits from the strengths of its base classifiers while effectively avoiding their weaknesses.