Geometric Algebra: Ascension of the Mind
I discovered Geometric Algebra (GA) back in 2003 and it caught my attention immediately. In my whole life as a student, engineer, researcher, and teacher I’ve never met a symbolic mathematical system so beautifully close to geometric abstractions. In this post, I try to explain how Geometric Algebra can express, unify, and generalize many geometric abstractions we use as engineers and computer scientists.
The Generative Pattern
There are many ways we can understand Geometric Computing depending on our background and intended applications. One of the ways I find most attractive is the pattern of Geometric Generators. To explain geometric generators, I will give some simple examples in 3D Euclidean geometry.
If we have 3 real numbers a, b, and c, what geometric concepts can we represent using these 3 numbers? The following are two possible answers that we can get from most engineers and computer scientists:
- A location in space: We are familiar with any point in our 3D Euclidean space being written as the 3-tuple (a, b, c).
- A direction in space: The same form of 3-tuple (a, b, c) can be also interpreted as a free vector in our geometric space.
The two concepts are related but have very different geometric semantics and a separate set of legal geometric operations for each. For example, vectors can be linearly combined (scaled and added) to get other vectors, adding two locations has no meaning geometrically, we can add a vector and a point to obtain a new point, etc. There is also some implicit information required to complete these two representations. We assume we have a basic set of 3 orthogonal axes that intersect at an origin point, we call that construction the coordinates frame. If we change the selected frame while keeping the geometric locations and directions as they are in relation to each other, we must update the 3-tuples numerically representing each location and direction in our problem. The main point here is that in order to generate a geometric location\direction in 3D Euclidean space we need to use 3 intersecting axes, common for all locations\directions, and 3 real numbers per location\direction. Then we need some algebraic operations, like linear and affine combinations, that we can use to generate a representation of a direction\location from these basic elements.
Let’s go one step further. If we have two locations P and Q, what can we geometrically generate in our selected space? The first thing we can think of is an infinite straight line; a line segment and a ray are related but different geometric concepts that can be generated by these same two points. What about a point C and a real number r? Maybe a sphere with center C and radius r, or a weighted-point (a location having mass, charge, or density associated with it). What about an infinite flat plane N and a non-parallel line L? We can generate the whole space from these two objects by “sliding” N along L. We can also generate a single location (their point of intersection), a single real number (the angle between L and N), a single line (the projection of L on N), a pair of infinite cones by rotating N around L, and many other geometric objects. Just by varying the geometric operations we use on N and L we generate new constructions. What if we have an infinitely extending cylinder? We can extract its axis (a line), its radius (a real number), we can generate many points on its surface (for example to approximate it using a triangular mesh), and we can slice it using flat planes to get circles, ellipses, or pairs of parallel lines.
Now we begin to see a simple pattern and we can abstract its main components:
- A set of Geometric Generators: A set of abstract geometric concepts that can be used to generate new geometric concepts. This set can be specified using abstract relations (arbitrary origin, orthogonal vectors of unit length, etc.), or can be explicitly represented using numbers (e.g. coordinates) relating them to (or generating them from) a common geometric frame of reference.
- A Geometric Algorithm: This is a sequence of steps to generate new geometric objects from the set of geometric generators. The new objects by themselves can be used as generators for more objects using other geometric algorithms; this includes the possibility of defining recursive algorithms and fractals.
- The Generated Geometric Concepts: By applying the geometric algorithm to the geometric generators we obtain new geometric objects of interest. This means that we can in principle use the set of generators in place of the generated concepts. For example, instead of listing all points on a line, we can simply state two points on the same line and the linear relation used for generating all the other points. Now we can transform the line (in the general sense of projective transformations for example) by transforming the generating set: its two points.
Anyone who worked with Generative Modeling 1 clearly recognizes and practices this pattern. This understanding is not so common, however, among engineers and computer scientists, especially in the early stages of their study and research. Most of us tend to lose sight of deep geometric abstractions hidden behind the many kinds of algebraic representations we are taught to use in our models. This creates serious problems on many levels for our geometric modeling abilities:
- On the level of understanding the true geometric nature of the problem.
- On the level of verifying the geometric model against possible algebraic, algorithmic, or numerical inconsistencies and special cases.
- On the level of generalizing the model to other problems or variations of the same problem.
- On the level of implementing the model as software.
- On the level of symbolically communicating our ideas effectively to other people.
We need to find an algebra that can be used to clearly express our generative pattern of geometry in a unified manner, independent of coordinates, and with algebraic relations generalizable to any space dimension.
An Algebra for Geometric Computing
For more than 100 years now we have been using many algebraic systems to symbolically and computationally encode our geometric intuition. Algebra enables the deduction of new relations between symbolic representations having geometric significance. Our bag of classical algebras we use to represent many essentially-geometric concepts and operations include:
- Vectors and Vector Spaces
- Matrices and Tensors
- Real Numbers
- Complex Numbers
- Many kinds of hyper-complex numbers like Quaternions, Octonions, Dual Numbers, Grassmann Numbers, and many others.
Using only one of these mathematical tools we can never model all aspects of geometric abstractions found in even a single problem of practical interest. We often need to use two or more of these algebras in our symbolic formulation of geometric ideas. Even worse, some geometric algorithms contain steps that are easier (or only possible) to represent using one algebra and\or set of generators, while other steps require a different algebra and\or set of generators 2. ًSo we need many algebraic representations for the same geometric concept, we need conversion steps between the representations. In effect, we need a huge number of algebraically ad-hoc techniques, whatever works, to solve our modeling problems. Sadly, we are completely lost in a jungle of symbolic abstractions, so what can we do?
Similar problems had been solved in some areas of engineering and computer science. Taking a quick look at problems modeled and solved with computers we find unifying algebraic systems at the core. For example:
- In database design, Relational Algebra is used for modeling the data stored in relational databases, and defining queries on it.
- In logic design, Boolean Algebra is fundamental in the development of digital electronics and is provided for in all modern programming languages.
- In data science, neural computing, computer graphics, and many other applications Matrix Algebra is the base of most computations.
- In optimization, simulation, and many other applications, the algebra of dual numbers is the base for implementing Automatic Differentiation, a much better practical replacement for numerical differentiation and finite difference methods.
For geometric computing, however, we don’t have a single unified algebraic system for our problems; this was my incorrect understanding until 2003 when I first read two online tutorials on Geometric Algebra 3. I discovered that all the above algebraic systems are isomorphic to some GA or one of its subalgebras, so we can seamlessly integrate them together. I discovered that most GA relations are geometrically significant and independent of space dimension and coordinate frames.
Since then I discovered firsthand how Geometric Algebra shines as an algebraic system that forces us to think about geometry from the generative perspective I described above. I experienced a high level of clarity, unification, and generalization of geometric ideas I’ve never felt before. Many ideas became connected immediately after formulating them in the language of Geometric Algebra. This experience is a true ascension of the geometric mind!
Almost all researchers working with Geometric Algebra have a similar experience. For example, Pablo Colapinto describes Geometric Algebra as 4:
Geometric algebra (GA) is a combinatoric system of spatial logic based on William Clifford’s hypercomplex algebras of the 19th century. Holistic, scalable, and filled with “common sense”, GA integrates various methods for modelling and engineering dynamic systems. […] The now classic work by the physicist David Hestenes, New Foundations for Classical Mechanics (1986) makes a strong argument for learning this approach by demonstrating the compactness of the math, while the most recent text by cyberneticist Eduardo Bayro-Corrochano, Geometric Computing: For Wavelet Transforms, Robot Vision, Learning, Control and Action (2010), demonstrates the expressivity of its powers for geometric reasoning. Many other references make a similar case: with its isomorphisms, geometric algebras encapsulate many other mathematical systems. With its outermorphisms, solutions worked out in smaller dimensions can often be extrapolated to higher dimensions. It is an expressive logic that allows intuitive mathematical experimentation across a widening range of disciplines.
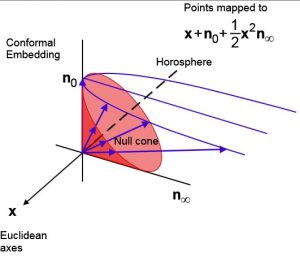
Working with the algebra, physicists have developed a conformal split mapping of a 3 dimensional Euclidean space G(3) into a 5-dimensional one, G(4,1), based on Riemannian projection of 3D Euclidean space (R3) onto a hypersphere. Introduced into the geometric algebra community by Hongbo Li, Alan Rockwood, and David Hestenes in 2001, the conformal model greatly simplifies and generalizes calculations of general rigid body movements in Euclidean space. As a mathematical system for describing closed form solutions within Euclidean, spherical, and hyperbolic geometries, conformal geometric algebra opens the door to a rich set of Möbius transformations typically restricted to the 2D plane. The operators which reflect, rotate, translate, twist, dilate, and boost other elements and objects are called versors.
The Universal Matrix
Many would argue that we can use matrices to represent all kinds of algebras used in practice including Clifford Algebras; an important subject in modern mathematics known as Representation Theory. This is true, theoretically speaking, but often impractical in many cases. The basic structure of a matrix and the simplicity of its addition and matrix multiplication operations is both a blessing and a curse.
Because matrices can represent many things, including raw lists\tables of numbers, we can use them as a universal low-level representation in our software implementations. Many numerical software systems used by engineers and computer scientists already do this: MATLAB, NumPy, ALGLIB, etc 5. In addition, many applications like computer graphics and robotics use homogenous-coordinate matrices as a universal representation for Euclidean, affine, and projective transformations. This is the good part, we can develop all our algorithms in the language of matrices based on Numerical Linear Algebra algorithms 6.
The prices we have to pay for using such simple universal algebraic structure are numerous, for example:
- Geometric Significance: Looking at an equation, expression or algorithm expressed as operations on matrices we often can’t easily understand its geometric significance. Many algebraic operations on matrices, like transpose, eigenanalysis, determinants, etc. are difficult to interpret in a geometrically meaningful way related to the original problem. In addition, expressing everything using matrices allows for incorrectly applying algebraic operations leading to geometrically meaningless results in the context of our problem. One example is obtaining complex eigenvalues when analyzing a real transformation matrix. These complex values can indicate errors in the algorithm, computational instabilities, or data that must be removed before doing the next step. Blindly accepting all outputs can cause many problems.
- Data Redundancy: For many geometric problems a full matrix representation is too much. Symmetric matrices, diagonal matrices, triangular matrices, and orthogonal matrices all contain numerical redundancies. As an example, one famous matrix representation of Conic Sections uses symmetric matrices. Passing this representation to a matrix processing software library may need memory and processing more than necessary.
- Extracting Geometric Information: Looking at the numbers inside a matrix we can’t immediately extract important geometric information. For example, given a homogeneous general rotation matrix, we can’t just find the axis and angle of rotation by looking at its numbers. We need to apply eigenanalysis to extract this important piece of geometric information.
- Geometric Type Safety: Compatibility rules for operations on matrices are too simple for modular software design. It might be algebraically acceptable, for example, to multiply two matrices, but geometrically wrong; resulting in an intermediate result that should have been automatically caught as a compile-time or run-time error. This may lead to many problems in verifying geometric algorithms and code debugging.
- Domain Specific Optimizations: Because matrices are numerically redundant, difficult to interpret geometrically, and low-level universal representations, it’s usually very difficult to apply high-level domain-specific optimizations to the geometric algorithm or computer code. This is one of the main reasons other kinds of algebra are used instead of matrices in many applications.
- Communication of Geometric Ideas: Teaching and communicating abstract geometric ideas using matrices is difficult. Matrix equations are good for low-level computations, but symbolically not suitable as a high-level language for expressing our geometric thoughts clearly. We need much training to look at a matrix equation in some application domain and understand its geometric meaning.
The Geometric Multivector
Many of these problems can be avoided using Geometric Algebra and its multivectors. GA has a much richer mathematical structure than matrix algebra as I will explain shortly. This sophisticated structure requires some time to learn but it’s logical and universal, so the learning time is well spent. Studying and using GA for several years I found many representational advantages of using multivectors over matrices, for example:
- Geometric Significance: Two main types of GA multivectors exist: Blades, and Versors. Blades can represent many geometric objects depending on the selected GA like directions, positions, lines, planes, hyperplanes, point-pairs, circles, spheres, tangent planes, conic sections, and much more. Versors can represent orthogonal transformations in the selected GA including translations, rotations, uniform scaling, affine and projective transformations, conformal transformations, and more. The geometric significance of multivectors is clear.
- Sparse Representation: Unlike matrices, GA’s multivectors representing significant geometric objects are practically sparse. This leads to the possibility of implementing many compiler optimizations to get the minimum possible sequence of computations required for some geometric algorithm.
- Extracting Geometric Information: The numerical components of many important multivectors are directly related to the geometric generators of the multivector. For example, it’s straightforward to extract the center and radius information from a Conformal GA multivector just be reading the coefficients of its basis blades. Much information can be extracted from multivectors using simple standard GA operations with direct and clear geometric meaning.
- Geometric Type Safety: Multivectors representing different geometric concepts usually contain different basis blades with non-zero coefficients. By simple inspection of a multivector, we can immediately understand its meaning and check its semantics. For example, the Conformal GA multivector representing a circle can have a radius with imaginary value. This indicates, for example, that two spheres do not intersect and the resulting multivector is of correct type: an imaginary circle with absolute radius related to the distance between the two spheres.
- Domain-Specific Modeling: Because of these beautiful properties, we can directly represent our high-level domain knowledge (i.e. Geometric Concepts and Algorithms) using GA’s operations on multivectors. Designing software systems for Geometric Computing can be on the same path that database design and logic circuits design took before.
- Communication of Geometric Ideas: GA’s symbolic multivector expressions are compact and geometrically significant. Just by knowing the meaning associated with multivectors in some expression we can easily follow, after some general application-independent training, its geometric significance. This feature makes teaching and geometric information exchange using Geometric Algebra a pleasant and mind opening experience.
Naturally, we need both matrix and multivector representations. We just need to select the most appropriate one for the problem. We may, for example, select to express our problem using multivectors for teaching purposes, while coding computations for the same problem with matrices at a later stage. The good news here is that we can create optimizing compilers that automatically generate matrices from GA operations on multivectors. We need to explore both methods of representation and never walk with the “hammer of matrices” as our only symbolic tool for dealing with all problems.
Geometric Algebra: The Way Ahead
Geometric Algebra is being explored in many applications, for example:
- Physics
- Computer Graphics
- Geometric Modeling
- Robotics
- Geographical Information Science
- Electromagnetics
- Computer Vision
- Neural Computing
- Automatic Theorem Proving
- Electrical Power Systems
- Signal and Image Processing
- Graph Theory
- Data Visualization
- Mechanical Engineering
Many opportunities exist for GA-based research and teaching, for example:
- Very few researchers develop efficient numerical algorithms for GA multivectors. Numerical Linear Algebra on matrices is much developed in comparison. We need to concentrate on this important task for creating efficient numerical algorithms to deal with multivectors.
- We need to reformulate and express common geometric modeling tasks using Geometric Algebra. For example, we need to write books on Computer Graphics or Robotics where each equation is expressed using GA multivectors, not matrices.
- We need to explore algorithmic and computational aspects of GA-based models. We need to design optimizing compilers that can understand and translate standard GA operations just like current compilers seamlessly understand floating point numbers.
- We need to use GA as a primary language for teaching geometric concepts in all sorts of engineering activities. The use of Geometric Algebra in schools is a big step towards the future of GA adoption and development.
In the following post, I will talk about the main mathematical elements of Geometric Algebra and how they integrate to create its full power and beauty. This kind of information is a good starting point for anyone new to the subject and in need for a clear roadmap to follow.
- See for example the Generative Modeling Language (GML) by Sven Havemann described in his very interesting Ph.D. dissertation. For a recent survey on this subject see “A Survey of Algorithmic Shapes” by Ulrich Krispel et al available here ↩
- For example rotations of vectors in 3D are best done using Quaternions while other affine transformations, especially composite ones, are better done using matrices! ↩
- Jaap Suter’s “Geometric Algebra Primer” and Mikael Nilsson’s “Geometric Algebra with Conzilla: Building a Conceptual Web of Mathematics” ↩
- In his 2011 M.Sc. thesis “VERSOR: Spatial Computing with Conformal Geometric Algebra” available here. ↩
- See the list of Freely Available Software for Linear Algebra composed by Jack Dongarra and Hatem Ltaief, University of Tennessee ↩
- Numerical Linear Algebra is the study of algorithms for performing linear algebra computations, most notably matrix operations, on computers. It is often a fundamental part of engineering and computational science problems, such as image and signal processing, telecommunication, computational finance, materials science simulations, structural biology, data mining, bioinformatics, fluid dynamics, and many other areas. Such software relies heavily on the development, analysis, and implementation of state-of-the-art algorithms for solving various numerical linear algebra problems, in large part because of the role of matrices in finite difference and finite element methods. ↩